Tension vers Température avec compensation soudure froide
Par équation (Méthode de Horner)
Par extraction des tables ITS-90 (Dichotomie & interpolation)
La colonne Table peut donner une valeur alors que la colonne Équation est en Erreur : Hors gamme, cela est dû aux limites différentes entre la recherche par table et le calcul par équation. Une case grisée dans la colonne Table montre une valeur exacte extraite des tables ITS-90, c'est-à-dire sans interpolation. Les valeurs de la colonne Écart sont calculées par rapport aux tables ITS-90. Les valeurs ohmiques sont celles d'une RTD DIN 43760 (100 Ω à 0 °C avec α = 0.00385 Ω/Ω/°C)
| CSF = Correction Soudure Froide | ||||||||
|---|---|---|---|---|---|---|---|---|
| Tension (mV) |
Type | Équation (°C) Sans CSF |
Table (°C) Sans CSF |
CSF (mV) Équation T = 0,00 °C |
CSF (mV) Table T = 0,00 °C |
Équation (°C) Avec CSF |
Table (°C) Avec CSF |
Écart (%) |
| 12,3450 | K | 303,302 | 303,293 | 0 | 0 | 303,302 | 303,293 | 0,0032 |
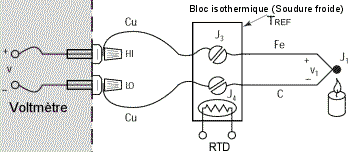
Explications : Nous avons déjà vu que : V = α(Tj1 - Tref)
V = Tension lue au voltmètre
α = Coeeficient de Seebeck
Tj1 = Température de la jonction du thermocouple
Tref = Température de la soudure froide
On en déduit que : V = αTj1 - αTref, c'est à dire : V = Vj1 - VJref
VJref est aussi nommé Vcompensation soudure froide)
Donc : Vjonction thermocouple = Vvoltmètre + Vcompensation
Le coefficient de Seebeck étant différent pour chaque type de thermocouple, il faut calculer la tension équivalente à la température de la soudure froide pour chaque type.
Pour les équations de conversion Ω vers °C des sondes platine RTD, voir le chapitre correspondant. Dans le cas présent, la conversion Ω vers °C est effectuée par interpolation de second ordre entre trois valeurs d'une table donnant les températures en fonction des valeurs ohmiques ; c'est la méthode la plus précise (+/- 0.003 °C)