Généralités sur les mesures
1. Mesurage d'une grandeur
Mesurer une grandeur, c'est la comparer à une grandeur de même espèce prise comme référence. Cette dernière constitue une unité de mesure ; l'ensemble des unités de mesures légales forme un système appelé Système International (SI).
En métrologie, domaine des connaissances relatives aux mesurages, le mot mesure a de nombreuses significations qu'il importe de préciser dès maintenant; il peut désigner :
- une valeur : la mesure d'une distance est de 100 mètres ;
- un résultat : mesure approchée à 1 % près ;
- une action : réaliser une mesure électrique ;
- un instrument: une mesure de capacité.
Pour éviter toute ambiguïté, il est préférable de parler respectivement de valeur d'une grandeur, de résultat de mesurage, de mesurage et de mesure matérialisée. Toutefois, lorsque aucune confusion n'est possible, on appelle mesure l'expression d'un résultat de mesurage.
2. Les Étalons
Un étalon est un instrument de mesurage destiné à définir ou matérialiser, conserver ou reproduire l'unité de mesure d'une grandeur (ou un multiple ou un sous-multiple de cette unité). Selon l'usage qui en est fait, plusieurs sortes d'étalons sont fabriquées. Pour une grandeur déterminée, l'étalon primaire est celui qui présente les plus hautes qualités métrologiques; il n'est jamais utilisé directement pour des mesurages en dehors de sa comparaison avec des étalons secondaires. À partir d'un étalon secondaire sont réalisés des étalons de travail qui sont utilisés pour vérifier les instruments de mesurage.
3. Erreurs des résultats de mesurages
On appelle erreur de mesurage la discordance entre le résultat du mesurage et la valeur de la grandeur mesurée.
Cette valeur peut être la valeur vraie ou, si celle-ci n'est pas connue (cas le plus fréquent), la valeur conventionnellement vraie de la grandeur, ou encore la moyenne arithmétique des résultats d'une série de mesurages. Cette discordance peut avoir des causes variées et, en général, on ne peut en déterminer qu'une limite supérieure, appelée incertitude de mesurage.
3.1. Erreur systématique
C'est une erreur qui reste constante en valeur absolue et en signe lorsque plusieurs mesurages d'une même grandeur fixe sont réalisés dans les mêmes conditions.
Les causes des erreurs systématiques peuvent être connues ou non. Si une telle erreur peut être déterminée par le calcul ou par l'expérience, on apporte une correction appropriée au résultat du mesurage. Si une erreur systématique ne peut pas être déterminée mais si sa valeur peut être supposée suffisamment petite par rapport à l'imprécision de mesurage, on la traite comme une erreur fortuite ; au contraire, si elle est supposée très supérieure à l'imprécision de mesurage, elle est évaluée approximativement et prise en compte dans le calcul de l'erreur.
Exemple d'erreur systématique : mesurage d'une masse à l'aide d'une masse marquée supposée égale à 1 kg, alors que sa masse vraie est 1,005 kg.
3.2. Erreur fortuite
C'est une erreur qui varie de façon imprévisible en valeur absolue et en signe lorsqu'on effectue un grand nombre de mesurages d'une même grandeur dans des conditions pratiquement identiques. On ne peut pas tenir compte d'une erreur fortuite en apportant une correction au résultat brut du mesurage. À la fin d'une série de mesurages, on peut seulement fixer une limite supérieure pour cette erreur.
Une erreur fortuite est souvent appelée erreur accidentelle ou erreur aléatoire.
3.3. Erreur parasite
C'est une erreur souvent grossière qui résulte d'une exécution incorrecte du mesurage. Par exemple, elle peut être due à une lecture fausse, ou à l'usage d'un instrument devenu défectueux, ou encore au mauvais emploi d'un instrument.
3.4. Erreur partielle
Au cours d'un mesurage déterminé plusieurs erreurs peuvent être commises : erreur due à l'appareil de mesurage, erreur due aux accessoires de l'appareil de mesurage, erreur de lecture, etc. Ces erreurs sont appelées erreurs partielles. L'incertitude de mesurage doit permettre de tenir compte de toutes les erreurs partielles en les composant selon une certaine loi qui sera exposée par ailleurs.
3.5. Erreur absolue
C'est la différence algébrique dx entre le résultat du mesurage X et la valeur de comparaison qui peut être la valeur vraie Xv ou conventionnellement vraie, ou la moyenne arithmétique x des résultats d'une série de mesurages. Dans le premier cas, l'erreur absolue est dite véritable (dx = X - Xv) ; dans le deuxième, elle est dite apparente (dx = X - x).
3.6. Erreur relative
C'est le quotient de l'erreur absolue et de la valeur de comparaison utilisée pour le calcul de l'erreur absolue (dx/Xv ou dx/x).
3.7. Écart quadratique moyen ou écart-type
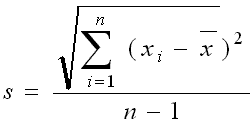
Dans une série de n mesurages d'une même grandeur, on caractérise la dispersion des résultats obtenus par l'écart quadratique moyen s qui est donné par la formule ci-contre.
si l'on désigne par Xi le résultat de mesurage de numéro i (i = 1,2,3,...,n) et par x la moyenne arithmétique des n résultats considérés.
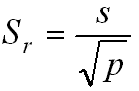
Si l'on réalise p séries de mesurages, on peut aussi définir l'écart quadratique moyen (écart-type) de la moyenne arithmétique d'une série de mesurages Sr :
Cet indice caractérise la dispersion de la moyenne arithmétique de la série de mesurages.
Remarque : l'augmentation du nombre de mesurages permet de diminuer l'importance des erreurs fortuites et une moyenne des résultats peut être acceptée comme résultat d'une série de mesurages.
4. Incertitudes. Loi De Composition
L'obtention d'un résultat de mesurage d'une grandeur x peut nécessiter une ou plusieurs opérations. Le mesurage d'une tension se réduit à une lecture sur un voltmètre, tandis que celui d'une résistance par une méthode voltampèremétrique impose une lecture U sur un voltmètre et une autre I sur un ampèremètre, le résultat étant donné par le quotient U/I. Le premier mesurage est dit direct, tandis que le second est dit indirect car le résultat est obtenu en combinant, selon une loi déterminée, des résultats de mesurages directs.
Pour un mesurage direct, la limite supérieure de l'erreur doit être évaluée en tenant compte du matériel utilisé et des conditions expérimentales. L'incertitude de mesurage dépend de la classe de précision de l'appareil et de la précision avec laquelle la lecture peut être faite.
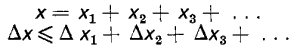
Pour un mesurage indirect, il faut rechercher les incertitudes correspondant aux divers résultats de mesurages directs à combiner et ensuite déterminer l'incertitude totale en considérant le cas où les erreurs ne se compensent pas (cas le plus défavorable). Dans le cas d'une somme ou d'une différence, on montre que l'incertitude absolue Δx est inférieure ou égale à la somme des incertitudes absolues :
Dans le cas d'un produit (ou d'un quotient) de grandeurs indépendantes, il est souvent nécessaire de chercher l'erreur commise à l'aide d'un procédé mathématique et de déduire ensuite l'incertitude comme on va le voir à présent. D'une façon générale, si une grandeur y est fonction de plusieurs autres a, b, c indépendantes, elle peut être assimilée à une fonction de plusieurs variables y = f(a, b, c). Les erreurs da, db, dc sur les variables étant très petites devant les valeurs respectives de ces variables, on peut les considérer comme des éléments différentiels et l'erreur entachant y est égale à la différentielle dy de la fonction f(a, b, c).
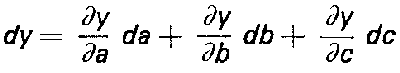
dy = (da * dérivée partielle de y par rapport à a) + (db * dérivée partielle de y par rapport à b) + (dc * dérivée partielle de y par rapport à c), ce que l'on écrit symboliquement sous la forme ci-contre.
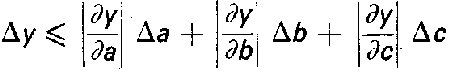
L'incertitude absolue Δy, limite supérieure de l'erreur, est obtenue en considérant que toutes les erreurs s'ajoutent, c'est-à-dire que tous les termes de la somme sont positifs :
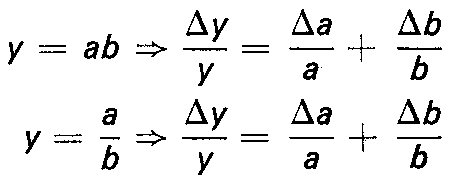
Δa, Δb, Δc étant les incertitudes avec lesquelles a, b et c sont connus. L'application de ce résultat montre que dans le cas de produits et de quotients de grandeurs indépendantes, l'incertitude relative Δy/y est égale à la somme des incertitudes relatives.
5. Erreurs, Qualités, Classe De Précision Des Appareils De Mesure Électriques
5.1. Erreur de base, erreur complémentaire
Les erreurs de mesurage dépendent d'un certain nombre de grandeurs dites d'influence comme, par exemple: la température, la pression, la position de l'appareil, le champ magnétique, etc. L'erreur de base d'un appareil de mesure électrique est celle qui est introduite lorsqu'on utilise cet appareil dans des conditions dites de référence, fixées par le constructeur. Au contraire, les erreurs complémentaires sont celles qui proviennent du fait que les valeurs des grandeurs d'influence sont différentes de celles qui correspondent aux conditions de référence.
Pour un appareil électromécanique, les principales erreurs de base sont dues aux frottements d'éléments mobiles sur des parties fixes, à l'inertie mécanique, à l'inertie thermique, à des erreurs de lecture, notamment à l'erreur de parallaxe (si l'index est à une certaine distance de la surface de l'échelle et que l'observateur ne peut se placer normalement à cette surface). Une courbe d'étalonnage est fournie par le constructeur pour les appareils de qualité : elle exprime la correspondance entre les valeurs de la randeur mesurée et les valeurs indiquées par l'appareil. Éventuellement, des courbes de corrections permettent de corriger les résultats obtenus lorsqu'une ou plusieurs grandeurs d'influence ne sont pas dans les conditions de référence.
5.2. Qualités d'un appareil de mesure
Plusieurs qualités sont à considérer pour juger un appareil de mesure.
- La justesse caractérise l'aptitude d'un appareil à donner des indications égales à la valeur vraie de la grandeur mesurée, c'est-à-dire non entachées d'erreurs systématiques
- La fidélité caractérise l'aptitude d'un appareil à donner des indications concordantes, donc non entachées d'erreurs fortuites pour une même grandeur mesurée.
- La sensibilité exprime quelle est la plus petite quantité dx qui peut être mesurée pour une valeur déterminée x de la grandeur mesurée. Cette sensibilité peut être constante le long de l'échelle. On remarquera que la sensibilité est d'autant plus grande que le nombre dx est faible.
- L'hystérésis ou réversibilité caractérise l'aptitude d'un appareil à donner la même indication lorsqu'on atteint une même valeur de la grandeur mesurée par valeurs croissantes ou par valeurs décroissantes.
- Le temps de réponse d'un appareil est le temps qui s'écoule entre une variation brusque de la grandeur à mesurer et l'instant où l'instrument donne une indication définitive de la nouvelle valeur de la grandeur.
- La précision d'un appareil de mesure est égale au rapport dx/x de l'erreur globale dx et de la valeur x de la grandeur à mesurer. Elle caractérise la qualité d'un instrument du point de vue des erreurs; la précision est d'autant plus grande que les indications sont plus proches de la valeur vraie (c'est-à-dire que dx est petit).
- La résolution, employée pour les appareils à affichage numérique, exprime la plus petite valeur qui peut être affichée. À ne pas confondre avec la sensibilité ou la précision.
5.3. Étendue de mesure, calibre d'un appareil
L'étendue de mesure d'un appareil est l'ensemble des valeurs pour lesquelles les indications obtenues ne sont pas entachées d'une erreur supérieure à l'erreur maximale tolérée. Certains instruments peuvent avoir plusieurs étendues de mesure.
Le calibre d'un appareil est la valeur de la grandeur à mesurer qui correspond à la limite supérieure de l'étendue de mesure. Par exemple, pour un ampèremètre, si cette limite supérieure est 5 A, on dit que son calibre est de 5 A.
5.4. Classe de précision
Un appareil de mesure (et ses accessoires) est caractérisé au moyen d'un nombre, appelé indice de classe. Celui-ci représente la limite supérieure de l'erreur absolue intrinsèque (c'est-à-dire due à l'appareil seul, utilisé dans les conditions de référence) exprimée en centièmes de la plus grande indication que peut donner l'appareil.
Ainsi, par exemple, un ampèremètre de classe 0,2 est un appareil dont l'erreur absolue intrinsèque ne dépasse pas 0,2 % de son indication la plus grande, lorsqu'il est utilisé dans des conditions normales. Si cet ampèremètre comporte 100 divisions, cette erreur absolue 0,2 intrinsèque est donc égale ou inférieure à 0,2/100*100= 0,2 division.
Pour un appareil à plusieurs calibres, ce résultat reste le même quel que soit le calibre ; en revanche, l'expression de cette erreur en ampères change avec celui-ci puisque 0,2 division d'une graduation qui en comporte 100 représente 0,2/100 du calibre (0,002 A pour le calibre 1 A) ; 0,01 A pour le calibre 5 A).
Les valeurs des indices de classe sont fixées par la norme NF C 42-100. Des appareils de même indice de classe sont dits de même classe de précision. Les appareils de classe 0,1 ou 0,2 sont dits étalons ; ceux de classe 0,5 sont des appareils de laboratoire. Les appareils de classe 1,5 ou 2,5 sont des appareils de contrôle.