Mesurer la tension produite par un thermocouple
Maintenant que nous savons qu'un thermocouple génère une tension dont la valeur est fonction de la température et du coefficient de Seebeck (α) de la jonction des deux métaux dissemblables, il ne reste plus qu'à mesurer celle-ci à l'aide d'un voltmètre puis d'exprimer, par calcul, la tension mesurée en température.
Connexion sur un voltmètre
Connectons un thermocouple Cuivre/Constantan (Type T)sur les bornes d'un voltmètre et, après calcul d'après α = 38,75µV/°C, nous trouvons une valeur de température qui n'a rien à voir avec l'ambiance dans laquelle se trouve le thermocouple.
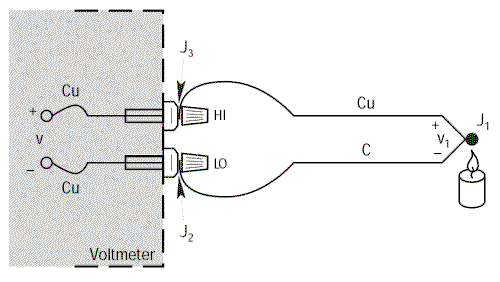
En connectant le thermocouple Cuivre/Constantan sur les bornes en cuivre du voltmètre, nous avons créé deux nouvelles jonctions métalliques : J3, jonction cuivre sur cuivre qui ne crée par de tension thermoélectrique et J2 qui, étant constituée de deux métaux différents (Cuivre/Constantan) génère une tension thermoélectrique (V2) qui vient en opposition avec la tension V1 que nous voulions mesurer.
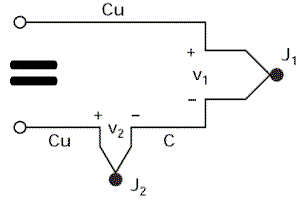
En fin de compte, en se référant au schéma équivalent (=), la tension résultante mesurée par le voltmètre est égale à V1 - V2, c'est-à-dire qu'elle est proportionnelle à la différence de température entre J1 et J2.
Référence de la jonction externe
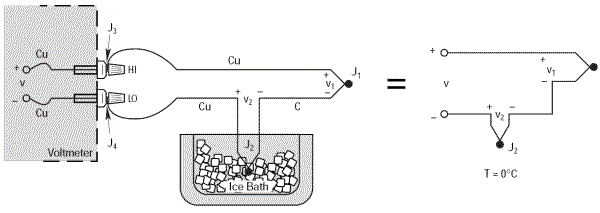
Une manière simple de déterminer exactement et facilement la température de la jonction J2 est de la plonger dans un bain de glace fondante, ce qui force sa température à 0°C (273,15 K). On pourra alors considérer J2 comme étant la jonction de référence.
Le schéma a donc maintenant une référence 0°C sur J2.
La lecture du voltmètre devient: V = (V1 - V2) équivalent à α (tJ1 - tJ2).
Écrivons la formule avec des degrés Celsius : Tj1 (°C) + 273,15 = tj1(K).
Et la tension V devient : V = V1 -V2 = α [(tJ1 + 273,15) - (tJ2 + 273,15)] = α (TJ1 - TJ2) = α (TJ1 - 0) = αTJ1
Nous avons utilisé ce raisonnement pour souligner que la tension V2 de la jonction J2, dans le bain de glace, n'est pas zéro volt. C'est une fonction de la température absolue. Cette méthode est très précise car la température 0°C (Point de fusion de la glace), peut être facilement et précisément contrôlée.
Le point de fusion de la glace est utilisé par les organismes de normalisation comme point de référence fondamental pour leurs tables de tension de thermocouple. Ainsi, à la lecture de ces tables, nous pourrons convertir directement la tension V1 en température TJ1.
C'est une fonction de la température absolue.
Et avec un autre type de thermocouple ?
Les exemples précédents ont été présentés avec un thermocouple Cuivre/Constantan (Type T), qui peut sembler d'une utilisation facile pour les démonstrations car le cuivre est également le métal des bornes du voltmètre et cela n'induit qu'une seule jonction parasite.
Effectuons le même exemple avec un thermocouple Fer/Constantan (Type J) à la place du Cuivre/Constantan.
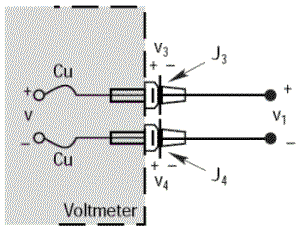
Le nombre de jonctions métalliques dissemblables augmente car les deux bornes du voltmètre sont maintenant composées de jonctions thermoélectriques Fer/Cuivre.
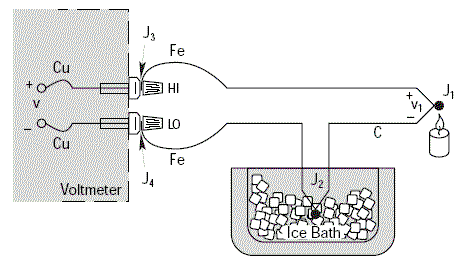
Le voltmètre indiquera une tension V égale à V1 seulement si les tensions thermoélectriques V3 et V4 sont identiques, puisqu'elles sont en opposition ; c'est-à-dire si les jonctions parasites J3 et J4 sont à la même température.
S'affranchir du problème des bornes du voltmètre
Pour éviter toute dérive de mesure, il est indispensable que les bornes de connexion du voltmètre soient à la même température.
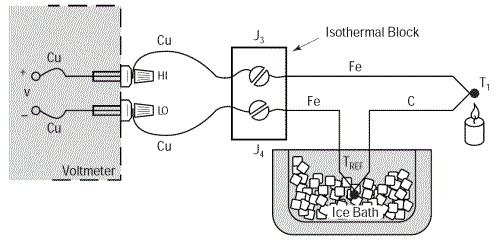
On peut éliminer ce problème en rallongeant les fils de cuivre pour ne les raccorder qu'au plus près du thermocouple avec un bloc de jonction isothermique.
Un bloc de ce type est un isolant électrique mais un bon conducteur de la chaleur de manière à maintenir, en permanence, les jonctions J3 et J4 à une température identique.
En procédant ainsi, nous pourrons, très facilement et sans problèmes, éloigner le thermocouple du moyen de mesure. La température du bloc isothermique n'a aucune importance puisque les tensions thermoélectriques des deux jonctions Cu-Fe sont en opposition.
Éliminer le bain de glace fondante
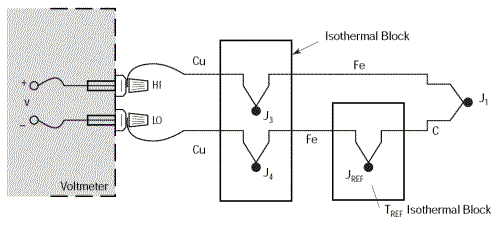
Le circuit précédent nous permet d'effectuer des mesures précises et fiables loin du thermocouple, mais quelle riche idée ce serait d'éliminer la nécessité du bain de glace fondante.
Commençons par remplacer le bain de glace fondante par un autre bloc isothermique que l'on maintiendra à la température TREF.
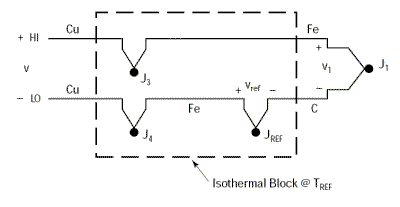
Puisque nous avons vu précédemment que la température du bloc isothermique supportant les jonctions J3 et J4 n'avait aucune importance - à condition que ces deux jonctions soient à la même température - rien ne nous empêche de réunir les deux blocs en un seul qui sera maintenu à la température TREF
Ce nouveau circuit présente, quand même, l'inconvénient de demander la connexion de deux thermocouples.
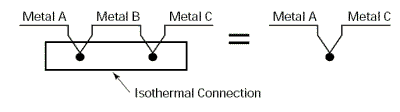
Nous pouvons très bien éliminer le thermocouple supplémentaire en combinant les jonctions Cu-Fe (J4) et Fe-C (JREF). Ceci est possible grâce à la loi des métaux intermédiaires. Plus de détails
Cette loi empirique stipule qu'un troisième métal (en l'occurrence du Fer) inséré entre les deux métaux différents d'un thermocouple n'a aucune influence sur la tension générée à condition que les deux jonctions formées par le métal additionnel soient à la même température.
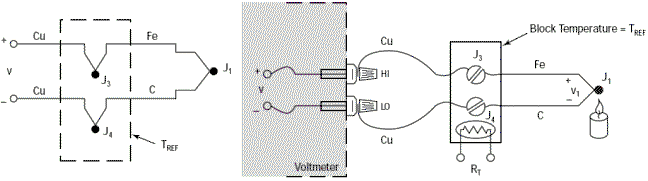
Nous en arrivons donc au circuit équivalent ci-dessous dans lequel nos deux jonctions J3 et J4 deviennent la Jonction de Référence et, pour lequel, la relation : V = α(TJ1 - TREF) est toujours vérifiée.
Récapitulatif
Nous avons, dans l'ordre :
- Créé une Jonction de Référence,
- Montré que V = α(TJ1 - TREF),
- Mis la Jonction de Référence dans un bain de glace fondante,
- Supprimé le problème des bornes du voltmètre,
- Combiné le circuit de référence,
- Éliminé le bain de glace fondante,