2.5. Le dispositif RESOLVER
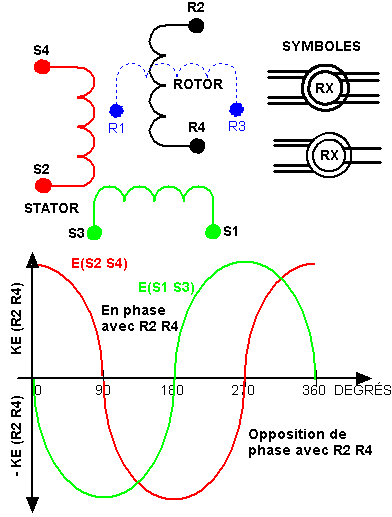
RESOLVER (Schéma et courbes de tension)
Le resolver, souvent intitulé synchro-resolver, est constitué, tout comme le synchro, d'un rotor et d'un stator et, si on le désigne également par le nom de trigonomètre, c'est parce que le stator est composé de deux enroulements en quadrature qui donnent, par les amplitudes des tensions induites, les sinus et cosinus de l'angle de rotation de l'axe du rotor.
E (S2 S4) = KE(R2 R4) Sin ωt Cos Θ
E (S1 S3) = KE(R2 R4) Sin ωt Sin Θ
K étant le facteur de couplage entre primaire (R2 R4) et les secondaires (S2 S4 et S1 S3) de la fonction transformateur, ω étant la pulsation (2.π.fréquence) de la tension d'excitation et Θ étant l'angle de rotation de l'axe du rotor en sens anti-horaire, vue du bout de l'axe, avec l'origine 0° égale au zéro électrique.
Certains resolvers comportent deux enroulements rotoriques, eux aussi en quadrature, les bornes du second enroulement étant nommées R1 R3, comme montré sur la figure ci-contre en pointillés bleus.
On peut utiliser l'enroulement statorique S4 S2 comme référence, l'enroulement statorique S3 S1 étant en court-circuit (ou l'inverse en fonction des besoins), et l'on se sert des deux bobinages rotoriques R2 R4 et R1 R3 pour récupérer les fonctions sinus et cosinus.
Bien que les amplitudes des tensions prennent quatre fois la même valeur sur un tour complet, la détermination de la position angulaire est déterminée, dans les quatre quadrants, par les combinaisons des signes des sinus et cosinus qui sont considérés comme positifs lorsque la tension est en phase avec la référence et négatifs lorsque la tension est en opposition de phase avec la référence.
Calculs trigonométriques
Transformations de coordonnées
Un des emplois des resolver est le calcul trigonométrique (Computing resolver).
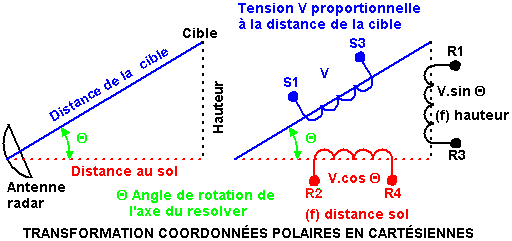
Par exemple, un resolver comportant deux enroulements statoriques et deux enroulements rotoriques, peut être utilisé pour effectuer des conversions de coordonnées polaires en coordonnées cartésiennes.
Supposons que les coordonnées polaires d'un point sont représentées par une tension E.sin ωt et un angle Θ. Si cet angle Θ est appliqué sur l'axe d'un resolver et la tension E.sin ωt appliquée sur un des enroulements statoriques comme référence, les tensions sur le rotor seront :
VR1-R3 = E.sin ωt.Sin Θ et VR4-R2 = E.sin ωt.Cos Θ.
Ces tensions représentent les coordonnées cartésiennes du point.
Rotations d'axes
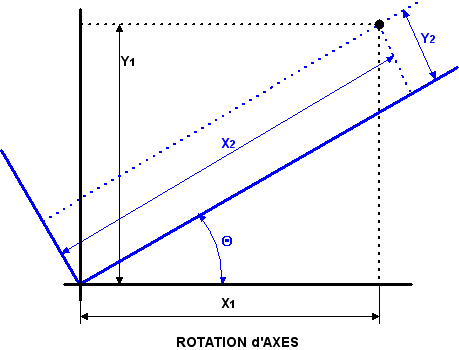
Supposons un point en espace euclidien représenté par ses coordonnées cartésiennes X1 et Y1. On déplace les axes originaux d'un angle Θ ; quelles seront alors les coordonnées du même point relativement au nouveaux axes X2 et Y2 ?
Tout mathématicien calcule facilement que ces nouvelles coordonnées sont :
X2 = X1 Cos Θ + Y1 Sin Θ
Y2 = Y1 Cos Θ - X1 Sin Θ
Ce calcul peut être effectué par un resolver avec un des enroulements statoriques alimenté par une tension fonction de X1 et l'autre par une tension fonction de Y1. Lorsque le rotor sera tourné d'un angle Θ, les tension présentes sur les enroulements rotoriques seront :
VR1-R3 = X1 Cos Θ + Y1 Sin Θ = X2
VR4-R2 = Y1 Cos Θ - X1 Sin Θ = Y2
Le resolver a effectué une transformation d'axes.
Synchro-Resolver, abus de langage
On entend et lit parfois le mot composé Synchro-resolver. C'est un abus de langage. Il est préférable de parler d'un côté de Synchro (trois enroulements stator à 120 degrés) et de l'autre de Resolver (deux enroulements stator à 90 degrés [fonctions sinus et cosinus]) qui, bien qu'étant tous les deux des systèmes de transmission de position ont des applications différentes.
Pour être comprise par un calculateur, une position transmise par un Synchro ou par un Resolver doit d'abord être décomposée en ses vecteurs trigonométriques sinus et cosinus, ce qui ne nécessite aucun autre dispositif pour un Resolver alors qu'il faut soit un transformateur de Scott, soit un circuit électronique pour un Synchro.
Les resolver ou trigonomètres sont plutôt utilisés pour la transmission d'angles compris entre 0 et 90 degrés car les amplitudes des tensions des enroulements donnent directement les fonctions sinus et cosinus sans s'occuper de la phase des signaux. On peut même, dans ce cas d'angle compris entre 0 et 90 degrés ne prendre en compte qu'un seul signal (sinus ou cosinus), ce qui, par rapport au synchro, simplifie les circuits et les calculs.