La mesure des distances dans le système solaire
Distance Terre-Lune Distance des planètes
LA DISTANCE TERRE-LUNE
À tout seigneur tout honneur. Nous allons établir les mensurations du plus beau et du plus poétique des astres. Je ne doute pas que notre poète Mannix parle de la Lune et je ne serais pas surpris qu'il nous en parle comme d'un bonheur à portée de la main.
Voici comment s'y sont pris deux astronomes français en 1751. Lalande s'est placé à Berlin (B) et Lacaille au cap de Bonne-Espérance (C) à une distance de 9000 km et pas trop loin du même méridien (il y a 5 ou 6 degrés d'écart entre Berlin et le cap de Bonne-Espérance). Ils étaient munis chacun d'une petite lunette et d'un fil à plomb. Chacun a mesuré l'angle formé par la direction de la Lune donnée par la lunette et la verticale du lieu d'observation donnée par le fil à plomb. Les deux mesures ont été faites le même jour au passage de la Lune au méridien.
Forts de ces mesures et connaissant la latitude de Berlin et du cap de Bonne-Espérance ils construisirent la figure suivante :
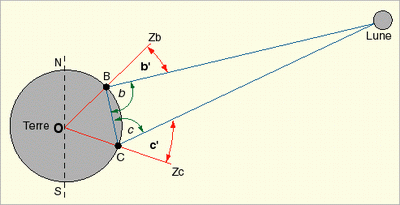
ZbO est la verticale en B (Berlin) et ZcO est la verticale en C (Cap de Bonne-Espérance) indiquées par le fil à plomb. C'est la latitude respectivement de B et C, que l'on nommera L1 et L2.
Donc l'angle BOC est la somme de ces 2 latitudes (en valeur absolue car Berlin est autour de 53 degrés N et le cap de Bonne-Espérance autour de 34 degrés S).
Donc BOC = L1 + L2
- L'angle OBC et l'angle OCB sont égaux car le triangle BOC est isocèle du fait que OB = OC = rayon de la Terre.
- Ils valent donc : [180 - (L1 + L2)] / 2 et on l'appellera d.
- b' est l'angle formé par la direction de la Lune et la verticale en B.
- c' sera l'angle formé par la direction de la Lune et la verticale en C. Ces deux angles sont donnés par la lunette.
- Ce qui permet d'écrire :
- Angle b = 180 - (b' + d)
- Angle c = 180 - (c' + d)
- Et l'angle formé entre B, la Lune et C est égal à 180 - (b + c).
- Nous l'appellerons P.
- Ayant ainsi déterminé l'angle P et connaissant la corde BC une simple application des règles de trigo donne la distance Terre-Lune.
- La moitié de la corde BC n'est autre que le sinus de la moitié de l'angle P - d'ailleurs le mot sinus signifie demi-corde.
Je n'ai pas retrouvé le chiffre que les deux astronomes ont calculé (en toises pour l'époque) mais tous les calculs qui ont été faits postérieurement avec cette valeur (et notamment le calcul des marées) montrent qu'il ne devait pas être loin de la réalité.
Lorsque l'angle P sous tend un diamètre entier de la terre, c'est l'angle sous lequel un observateur placé sur la Lune voit la Terre et la moitié de cet angle s'appelle LA PARALLAXE DE LA LUNE et vaut 57 minutes 3 secondes d'arc.
La distance Terre-Lune varie entre 363 000 et 405 000 km et l'on prend comme distance moyenne 384 000 km.
Aujourd'hui on peut mesurer cette distance directement avec un radar, ou un laser grâce à un réflecteur déposé sur la lune par une des missions Apollo, en mesurant la durée aller retour des impulsions-radars ou laser. La résolution du laser est de l'ordre du cm !
NOTA : La démonstration n'est rigoureusement vraie que si les longueurs B-Lune et C-Lune sont égales. Mais la figure n'est pas à l'échelle et l'angle P est très petit, de plus l'histoire ne le dit pas, mais étant donné la qualité des deux astronomes on peut penser qu'ils ont choisi une date où justement la hauteur de la Lune par rapport à l'équateur terrestre satisfaisait au mieux cette condition. De toute façon l'erreur ne pourrait pas dépasser 800 km ce qui reste petit devant les 384 400 km et de plus on peut en tenir compte a posteriori.
Avec cette distance maintenant établie, il est facile de déterminer le diamètre de la Lune.
Mais justement, parlons-en du diamètre de la Lune. Si vous interrogez votre entourage, certains vous diront la Lune est grande comme un ballon de foot, d'autres diront comme une assiette, d'autres comme une pièce d'un Euro, d'autres rapporteront la Lune comme une montgolfière. Tout cela ne veut rien dire. L'impression reçue par ces personnes ne signifie rien quant à la grandeur réelle de la Lune. Ce qu'elles expriment n'est rien d'autre que la grandeur apparente ou le diamètre angulaire apparent de la Lune dont il est facile de mesurer la valeur avec une petite lunette montée sur quart de cercle gradué en degrés. Vous trouverez suivant le moment de la mesure entre 29 minutes 22 secondes et 32 minutes 46 secondes.
Maintenant, regardez un rapporteur d'angle d'écolier. Il est constitué d'un demi-cercle dont le rayon est généralement de l'ordre de 50 à 60 mm et les degrés y ressemblent fort à des mm.. Ce n'est pas surprenant car pour un rayon de 57,3 mm la circonférence mesure 360 mm soit 1 mm par degré.
Ainsi 1 degré est représenté par 1 mm à 57,3 mm ou 10 mm à 573 mm ou 100 mm à 5,73 m ou 100 m a 5,73 km et à 384 000 km on trouve : 100m x 384 000/5,73 = 3 462 km.
Le chiffre retenu est 3 474,6 km pour le diamètre équatorial moyen.
Avec le diamètre, nous connaissons son volume et en application des règles sur la gravité énoncées par Newton, les marées qu'elle imprime à la Terre permettent de calculer sa masse et donc sa densité moyenne.
Voici donc la Lune déjà pas mal déshabillée. Avouez qu'avec une simple lunette et un fil à plomb c'est pas mal !
René Paris - Promotion 50-53 + Radio
LA DISTANCE DES PLANÈTES
Les planètes dans l'ordre croissant de leur distance au soleil s'échelonnent comme il suit : Mercure, Venus, la Terre, Mars, Jupiter, Saturne, Neptune, Pluton. La dernière, Pluton a été récemment rétrogradée de son rang de planète sous le fallacieux prétexte qu'elle est trop petite pour mériter ce titre. Mais comme elle est quand même trop grosse pour entrer dans le cercle des astéroïdes, on l'a rebaptisée planète naine. La belle affaire...!
C'est à Kepler, l'un des piliers de l'astronomie de position, que l'on doit d'avoir compris que les planètes décrivent des ellipses dont le soleil occupe l'un des deux foyers, (le mot foyer ne peut pas être mieux choisi pour le soleil).
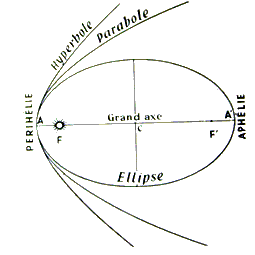
Le grand axe et le petit axe sont axes de symétrie de l'ellipse. Ils se coupent perpendiculairement en leur milieu et déterminent ainsi le centre de l'ellipse. Les 2 foyers F et F' sont situés sur le grand axe à égale distance du centre. Le quotient de la distance qui sépare les 2 foyers par la longueur du grand axe s'appelle l'excentricité que l'on nomme habituellement e = FF' / AA'.
L'excentricité des planètes est faible, celle de la Terre est 0,0167. Le cercle est une ellipse particulière dont les 2 foyers sont confondus au centre. L'excentricité est donc nulle.
En ce qui concerne les planètes, le point où elles passent au plus près du foyer où se trouve le soleil s'appelle le périhélie (de péri = autour) et le point où elles passent au plus près de l'autre foyer donc au plus loin du soleil s'appelle l'aphélie (du grec apo = loin).
Revenons à Kepler, il le mérite. Kepler (1572 - 1630) fut l'assistant de 1600 à 1601 de Tycho Brahé (1546 -1601) qui était un formidable observateur dont les innombrables mesures astronomiques étaient d'une remarquable qualité pour l'époque. C'est par un travail acharné d'analyse de ces mesures que Kepler découvrit les lois qui désormais portent son nom.
Première loi dite des orbites : les planètes décrivent des ellipses dont le soleil occupe l'un des foyers.

Deuxième loi dite loi des aires : les surfaces décrites par les rayons vecteurs sont proportionnelles aux temps employés à les balayer. Sous une autre forme : les surfaces balayées par les rayons vecteurs en des temps égaux sont égales. Elle implique que la vitesse de la planète varie avec la position qu'elle occupe sur son orbite. Elle est la plus rapide à son périhélie et la plus lente à son aphélie. Si les segments AB, CD, et EF sont parcourus en des temps égaux, les surfaces balayées BSA, CSD, et ESF sont égales Fig. ci-contre.
Troisième loi dite loi des périodes : le carré du temps de révolution des planètes est proportionnel au cube du grand axe.
Le champ de bataille est maintenant déterminé.
La première mesure qui semble facile à faire est celle de la durée de révolution de chaque planète.
Quand on veut connaître le temps que met un cycliste pour faire un tour de piste, c'est facile, il suffit de déclencher le chronomètre lorsque le cycliste passe sur la ligne de départ et de l'arrêter à l'instant où il repasse sur cette ligne. Mais dans le ciel il n'y a pas de ligne de départ et le chronométreur tourne aussi sur une autre piste puisqu'il est sur la Terre.
Les astronomes qui sont des gens futés, avaient remarqué depuis très longtemps que lorsque les jours plus longs que les nuits se produisaient dans l'hémisphère nord, c'était l'inverse dans l'hémisphère sud et vice versa. Il y a donc un moment où la durée du jour égale exactement la durée de la nuit. À la fin de l'hiver, si on suit le soleil avec une petite lunette (attention les yeux) de jour en jour, on observe que sa trajectoire se rapproche progressivement de l'équateur par "en dessous" puis qu'un certain jour elle passe au-dessus. L'instant où la trajectoire du soleil coupe l'équateur dans le sens que l'on vient de voir s'appelle l'équinoxe de printemps et il y a égalité du jour et de la nuit sur toute la surface de la Terre. Il y a aussi un équinoxe d'automne lorsque le soleil venant du dessus coupe l'équateur pour passer dessous. Ces instants sont très précis et le temps qui s'écoule entre deux équinoxes de printemps successifs est de 365 jours 5 heures 48 minutes et 45,67 secondes. Vous avez reconnu la durée de l'année.
La durée de révolution de le Terre étant maintenant déterminée, il est aisé de trouver celle des autres planètes. Si pendant que la Terre parcourt 10 degrés sur son orbite vous constatez qu'une autre planète ne fait que 5 degrés vous en concluez qu'elle mettra 2 fois plus de temps que la Terre pour accomplir son orbite totale (et lycée de Versailles comme dirait Frédéric Dard).
Ceci est le principe de la mesure, dans la réalité c'est un peu plus compliqué, mais c'est affaire de spécialistes et ça n'apporterait pas grand-chose au commun des mortels.
Voici la durée de révolution de chaque planète en jours terrestres.
- Mercure : 88 j
- Vénus : 225 j
- Mars : 1an et 322 j
- Jupiter : 11 ans et 315 j
- Saturne : 29 ans et 167 j
- Uranus : 84 ans et 7 j
- Neptune : 164 ans et 280 j
- Pluton : 248 ans et 154 j
Avec ces durées de révolution et en application de la 3e loi de Kepler (le carré de la durée de révolution des planètes est proportionnel au cube du grand axe de l'ellipse), on peut directement déduire le rapport qui existe entre le grand axe de l'orbite de chaque planète et celui de l'orbite terrestre.
En prenant comme unité le grand axe de l'orbite de la Terre et en appelant x les grands axes cherchés, on a :
Pour Mercure : 88 x 88 / 365 x 365 = x au cube d'où x = 0,387.
Pour Vénus : 225 x 225 / 365 x 365 = x au cube d'où x= 0,723.
Et pour Mars, Jupiter, Saturne, Uranus, Neptune et Pluton, on trouverait respectivement : 1,524 - 5,203 - 9,555 - 19,218 - 30,110 - 39,518.
Mais direz-vous ces distances prennent comme unité la distance Terre Soleil mais ce que nous aimerions connaître ce sont ces distances en km ! Qu'à cela ne tienne, mesurons la distance Terre-Soleil et le tour sera joué.
Alors les astronomes se sont mis au travail et ils ont voulu appliquer la méthode qui leur avait si bien réussi pour la Lune (voir l'article sur la distance de la Lune). Ils ont vite compris que même en prenant comme base du triangle la longueur totale d'un diamètre de la Terre, la parallaxe du soleil conduit à un angle si petit que compte tenu des incertitudes de mesure, il est illusoire d'en tirer quoi que ce soit. Mais intrépides comme sont les astronomes, certains n'hésitèrent pas à donner des chiffres. Le grand Kepler proposa 45 millions de km. La Hire avança 219 millions de km. Prudemment on en resta là !
Cassini suggéra qu'au lieu de mesurer la distance Terre-Soleil, il suffisait de mesurer la distance entre la Terre et une planète proche et en application de la 3e loi de Kepler, on trouverait toutes les autres distances (résolution d'une équation du 3e degré). Les planètes les plus proches de la Terre sont Vénus et Mars. Mais même avec ces plus "proches" la mesure précise est impossible. Il fallut attendre la découverte en 1898 d'une petite planète (un astéroïde) que l'on baptisa Eros et qui s'approche de la Terre beaucoup plus près que Mars et Vénus. En 1901, Eros passa "seulement" à 18 300 000 km de la Terre. Les astronomes firent feu de toutes leurs pièces. Bref et pour ne pas assommer l'auditoire avec "les détails de l'histoire" la distance Terre-Soleil fut établie à 149 500 000 km et baptisée unité astronomique (UA).
De cette distance on déduisit immédiatement les distances de toutes les planètes.
Le mouvement de la Terre étant soumis à toutes sortes de perturbations dont l'une des principales est l'attraction des autres planètes, l'ellipse décrite par la Terre n'est pas aussi pure qu'on pourrait le croire et de ce fait son demi grand axe est quelque peu variable. Pour une longueur prise comme unité, on a jugé que ce n'était pas convenable. On a donc calculé une longueur toute théorique à partir d'une Terre non moins théorique ponctuelle et de masse nulle ! Corroborée par des mesures au radar et l'observation de la trajectoire des sondes spatiales, l'unité astronomique est établie à 149 597 870, 691 km à plus ou moins 30 m.
Retenez 150 millions de km et tout le monde sera content !
Roemer, qui en 1676 avait fait une mesure de la vitesse de la lumière avec pour la première fois une méthode sérieuse, imagina un moyen ingénieux et intéressant pour déterminer la distance Jupiter-Soleil. Intéressant car faisant appel à un principe totalement différent de la trigonométrie. Je mentionnerai qu'il a établi la vitesse de la lumière autour de 220 000 km/s et que la bonne vitesse de 300 000 km/s fut établie beaucoup plus tard avec exactement la même méthode simplement plus précise car utilisant un matériel dont la technique de fabrication était plus fine.

Donc Roemer observait Jupiter et en particulier ses 4 principaux satellites qui sont visibles dans la moindre petite lunette et qu'on appelle galiléens car découverts par Galilée. Ces satellites en tournant sagement autour de leur planète sont périodiquement éclipsés quand ils passent derrière Jupiter vu de la Terre. Il mesura le temps qui s'écoulait entre deux éclipses consécutives (ce temps est relativement court et se chiffre en dizaines d'heures). Armé de ce nombre magique il put prédire le jour, l'heure, la minute et la seconde des éclipses futures. Qu'elle ne fut pas sa surprise de constater que ses prévisions étaient fausses de plusieurs minutes. Les satellites tourneraient-ils comme des patates ? Il contrôla que la durée entre deux éclipses consécutives était bien constante. Ouf, Kepler et Newton étaient sauvés. Ce qui variait c'est la date prévisionnelle des éclipses. Il mesura que ces éclipses se faisaient avec une avance de 8 mn et 19 s quand la Terre était au plus près de Jupiter et avec un retard de 8 mn et 19 s quand la Terre était au plus loin. Roemer, qui n'était pas bête, en déduisit que ce décalage de 16 mn et 38 s correspondait au temps que met la lumière à parcourir la distance entre le plus près et le plus loin de Jupiter donc le diamètre de l'orbite terrestre. La moitié de ce chiffre multiplié par la vitesse de la lumière donnera la distance de la Terre au soleil. Effectivement si on prend la vitesse de la lumière à 300 000 km/s on trouve 149 700 000 km. Pas mal !
Si vous aimez ça et que vous en redemandez, je vous parlerai une autre fois de la distance des étoiles et des galaxies.
Mais c'est une tout autre Histoire !
René Paris promo 50-53 + R