Règles d'emploi des unités
Noms d'unités
Tous les noms d'unités, mêmes ceux qui dérivent de noms de savants, sont considérés comme des noms communs : volt, ampère, henry, weber, watt, joule, pascal, newton, hertz, coulomb, etc. Les initiales s'écrivent en minuscules et ils prennent la marque du pluriel s'ils suivent un nombre égal ou supérieur à 2 : 1,9 volt, 3 ampères, 1,4 newton, 5 watts, 3 henrys
Les noms des unités dérivées de noms de savants sont du genre masculin (un joule, un ampère, un henry). Aucun qualificatif ne doit être ajouté à un nom d'unité (on ne dit pas mètre linéaire).
Lorsqu'une grandeur est le produit de deux autres, dont aucune n'est un quotient, le nom de l'unité est obtenu en réunissant les deux unités correspondantes par un trait d'union (et surtout pas en plaçant une barre oblique, symbole d'un quotient). Par exemple, l'énergie électrique qui est le produit d'une puissance et d'un temps peut être exprimée en tant que watt-heure. Dans le cas d'unités très courantes, les deux noms peuvent être accolés : un wattheure ou un watt-heure. La marque du pluriel s'ajoute aux deux noms composants en cas de trait d'union et au seul dernier en cas de noms accolés : des watts-heures ou des wattheures, des mètres-newtons.
Lorsqu'une grandeur est le quotient de deux autres, qui ne sont pas elles-mêmes des quotients, le nom est obtenu en intercalant par (et non pas le symbole de la division) entre les unités du dividende et celles du diviseur : kilomètre par heure, mètre par seconde.
Symboles d'unités
En principe, tous les symboles des unités sont en minuscules mais, si le nom de l'unité dérive d'un nom propre, la première lettre du symbole est majuscule : N pour newton, J pour joule, Hz pour hertz, V pour volt, A pour ampère, etc. Le symbole du litre constitue une exception à cette règle. La 16e Conférence générale (1979, Résolution 6) a approuvé l'utilisation de la lettre L en majuscule ou l en minuscule comme symbole du litre, afin d'éviter la confusion entre le chiffre 1 (un) et la lettre l.
Si l'on utilise un préfixe de multiple ou sous-multiple, celui-ci fait partie de l'unité et il précède le symbole de l'unité, sans espace entre le symbole du préfixe et le symbole de l'unité. Un préfixe n'est jamais utilisé seul et l'on n'utilise jamais de préfixes composés.
Les symboles d'unités sont des entités mathématiques et pas des abréviations. Ils ne doivent donc pas être suivis d'un point, sauf s'ils se trouvent placés à la fin d'une phrase. Ils restent invariables au pluriel - 10 kg et non pas 10 kgs. et il ne faut pas mélanger des symboles avec des noms d'unités dans une même expression, puisque les noms ne sont pas des entités mathématiques.
À la suite d'un nombre, un nom d'unité peut être remplacé par son symbole : on peut écrire 5 mètres ou 5 m mais il faut écrire cinq mètres (et non pas cinq m). Un symbole est disposé obligatoirement à la suite du résultat numérique lorsqu'il s'agit d'unités décimales : 26,3 m (et non pas 26 m,3). Cette règle ne s'applique pas aux unités qui ne sont pas décimales : 12 h 15 mn 30 s.
Symboles composés
Dans le cas d'unités composées, le symbole est figuré par une expression algébrique dans laquelle chacun des symboles joue le même rôle que la grandeur correspondante de l'équation de définition; ainsi dans le cas de produit (vectoriel ou scalaire) ou de quotient, le symbole est le produit (vectoriel ou scalaire) ou le quotient des symboles des unités composantes. Par exemple à l'unité d'énergie électrique le wattheure correspond le symbole Wh.
Une vitesse, quotient d'une longueur et d'un temps, peut s'exprimer avec une unité dont le symbole est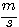 
(barre horizontale) ou m/s (barre oblique) ou m·s−1.
Le moment d'une force étant numériquement égal au produit vectoriel de l'intensité d'une force et d'une longueur, le symbole de l'unité de moment peut s'écrire m/N ou N.m. Il est à noter que selon l'ISO 31, le point situé entre les deux symboles devrait être à mi hauteur : N·m
II est à noter que l'expression obtenue peut être transformée en appliquant les règles de l'algèbre ; la résistivité électrique étant définie par l'expression RS/l où R est une résistance, S une surface et l une longueur, l'unité correspondante a pour symbole (Ω.m2)/m ou Ω.m après simplification. Des exposants positifs ou négatifs peuvent également être employés dans ces expressions : la masse volumique est le quotient d'une masse et d'un volume, l'unité a pour symbole kg/m3 ou kg.m−3.
Préfixes
Préfixes à utiliser devant le nom des unités pour en multiplier la valeur (kilomètre, centilitre, gigahertz). Les symboles sont à utiliser devant les symboles des unités (km, cl, GHz).
| Préfixe | Symbole | Facteur | Remarques |
|---|---|---|---|
| quetta | Q | 1030 |
Si l'un de ces préfixes est accolé au nom d'une unité simple à la première puissance il doit être considéré comme un multiplicateur de cette unité; sa valeur est la puissance de 10 indiquée dans le tableau (ex. : 1 km = 103 m). Si l'unité, à laquelle est accolée le préfixe, se trouve élevée à une puissance déterminée (ex. : un kilomètre carré), il faut considérer que c'est l'unité multiple ou sous-multiple qui doit être élevée à cette puissance: 1 km2= (1 km)2 = (103 m)2= 106 m2 (et non pas 103 m2). Le préfixe « myria », utilisé autrefois et qui correspondait au facteur 104 = 10 000, n'est plus mentionné et ne doit donc plus être employé. Ces préfixes SI représentent strictement des puissances de 10. Ils ne doivent pas être utilisés pour exprimer des multiples de 2 (par exemple, un kilobit représente 1000 bits et non 1024 bits).
|
| ronna | R | 1027 | |
| yotta | Y | 1024 | |
| zetta | Z | 1021 | |
| exa | E | 1018 | |
| peta | P | 1015 | |
| téra | T | 1012 | |
| giga | G | 109 | |
| méga | M | 106 | |
| kilo | k | 103 | |
| hecto | h | 102 | |
| déca | da | 101 | |
| - | - | 100 | |
| déci | d | 10−1 | |
| centi | c | 10−2 | |
| milli | m | 10−3 | |
| micro | µ | 10−6 | |
| nano | n | 10−9 | |
| pico | p | 10−12 | |
| femto | f | 10−15 | |
| atto | a | 10−18 | |
| zepto | z | 10−21 | |
| yocto | y | 10−24 | |
| ronto | r | 10−27 | |
| quecto | q | 10−30 |
Énoncé des très grands nombres
Pour énoncer les puissances de 10, à partir de 1012 on applique la règle exprimée par la formule :
106N = (N) illion.
| Nombre | Énoncé |
|---|---|
| 1012 | billion |
| 1018 | trillion |
| 1024 | quadrillion |
| 1030 | quintillion |
| 1036 | sextillion |
Préfixes pour multiples binaires
En décembre 1998, le BIPM (Bureau International des Poids et Mesures) et l'IEC (International Electrotechnical Commission), organisations internationales de normalisation, ont approuvés les noms et symboles à utiliser pour les multiples binaires employés en informatique et transmission de données.
| Préfixe | Symbole | Facteur | Valeurs et comparaisons |
|---|---|---|---|
| yobi | Yi | 280 | |
| zébi | Zi | 270 | |
| exbi | Ei | 260 | |
| pebi | Pi | 250 | |
| tebi | Ti | 240 | |
| gibi | Gi | 230 | Un gibibyte (gibioctet) GiB = 1 073 741 824 B (octet) Un gigabyte (gigaoctet) GB = 1 000 000 000 B (octet) |
| mebi | Mi | 220 | Un mebibyte (mebioctet) MiB = 1 048 576 B (octet) Un megabyte (megaoctet) MB = 1 000 000 B (octet) |
| kibi | Ki | 210 | Un Kibibit (Kibit) = 1024 bit - Un kilobit (kbit) = 1000 bit |
Alphabet grec
Les lettres de l'alphabet grec étant très fréquemment employées,
il est nécessaire de les rappeler.
| Lettre grecque | Nom | Correspondance | Lettre grecque | Nom | Correspondance |
Α α | alpha | A ou a | Ν ν | nu | N ou n |
Β β | bêta | B ou b | Ξ ξ | xi (ksi) | X ou x ou cs |
Γ γ | gamma | G ou g | Ο ο | omicron | O ou o |
Δ δ | delta | D ou d | Π π | pi | P ou p |
Ε ε | epsilon | é ou é | Ρ ρ | rhô | R ou r |
Ζ ζ | dzêta | DZ ou dz | Σ σ | sigma | S ou s |
Η η | êta | ê ou ê | Τ τ | tau | T ou t |
Θ θ | thêta | T ou th | Υ υ | upsilon | U ou u |
Ι ι | iota | I ou i | Φ φ | phi | F ou f |
Κ κ | kappa | K ou k | Χ χ | chi | K ou k |
Λ λ | lambda | L ou l | Ψ ψ | psi | PS ou ps |
Μ μ | mu | M ou m | Ω ω | oméga | ô ou ô |
Grandeurs
Une grandeur est tout ce qui est susceptible d'augmentation ou de diminution comme, par exemple, une longueur, une surface, une puissance, etc. Mesurer une grandeur G (quelle que soit son espèce), c'est la comparer à une autre grandeur U, de même espèce, choisie pour unité. Le résultat de la mesure est un nombre entier (par ex. 5) si l'unité U est contenue un nombre entier de fois dans la grandeur G considérée (5 fois ici).
Une grandeur est directement mesurable quand nous pouvons définir le rapport ou l'égalité et la somme de deux valeurs de cette grandeur. Une longueur, une surface sont des grandeurs mesurables. En revanche, une température repérée au moyen de l'échelle thermométrique Celsius n'est pas une grandeur mesurable : nous pouvons définir l'égalité de deux températures mais nous ne pouvons pas en faire la somme.
Unités de mesure
Pour mesurer les diverses grandeurs physiques, un certain nombre d'unités ont été définies. Des relations géométriques ou physiques (relation entre une surface et une longueur, relation entre une force et une masse, etc.) font que la plupart de ces unités dépendent de quelques-unes d'entre elles. Pour cette raison, dans un système d'unités de mesure, il faut distinguer les unités de base ou unités principales qui sont choisies arbitrairement (elles constituent les bases du système d'unités) et les unités secondaires définies à partir des précédentes. Les premières correspondent aux grandeurs fondamentales et les secondes aux grandeurs dérivées. À un système d'unités sont également adjointes quelques unités hors système ou unités auxiliaires d'usage courant mais limité à certains corps de métiers (l'électronvolt et le mille marin, par exemple).
Grandeurs fondamentales
Les grandeurs fondamentales utilisées pour les divers systèmes réservés aux grandeurs géométriques et aux grandeurs mécaniques sont en général au nombre de trois : une longueur, une masse et un temps. Les unités correspondantes diffèrent selon le système: ce sont le mètre, le kilogramme et la seconde pour le Système International, le centimètre, le gramme et la seconde pour le système C.G.S. Ces systèmes ont dû être complétés pour définir des unités pour les grandeurs électriques, magnétiques, lumineuses, etc., et plusieurs grandeurs fondamentales supplémentaires ont souvent été nécessaires ; par ex., pour le Système International, aux trois grandeurs fondamentales indiquées précédemment ont été ajoutées quatre autres : l'intensité du courant, la température thermodynamique, l'intensité lumineuse et la quantité de matière.
L'élaboration de systèmes cohérents d'unités de mesure s'est faite progressivement à partir des unités du système métrique. Bien que les définitions de ces unités aient dû être précisées pour la mise au point des systèmes d'unités utilisés de nos jours, elles conservent néanmoins un intérêt historique certain.
Remarque sur l'Unité de force :
Le poids d'un corps étant une force, il a été possible de prendre le poids du kilogramme étalon pour unité de force du système métrique (c'est la force avec laquelle cet étalon est attiré vers le centre de la Terre). Mais cette force d'attraction variant avec la latitude et l'altitude des points du globe, la Conférence générale des poids et mesures d'octobre 1907 a décidé que, par convention, cette unité de force n'était ainsi définie que pour tout point de latitude 45° et d'altitude zéro (niveau de la mer). La valeur correspondante de l'accélération de la pesanteur est g = 9,806 16 m/s2 alors qu'à Paris, l'accélération de la pesanteur a pour valeur 9,81 m/s2.