Astronomie - René Paris - Promotion 1950-1953

LA RÉALISATION DES MIROIRS POUR TÉLESCOPES D'AMATEURS

LA « PARABOLISATION »

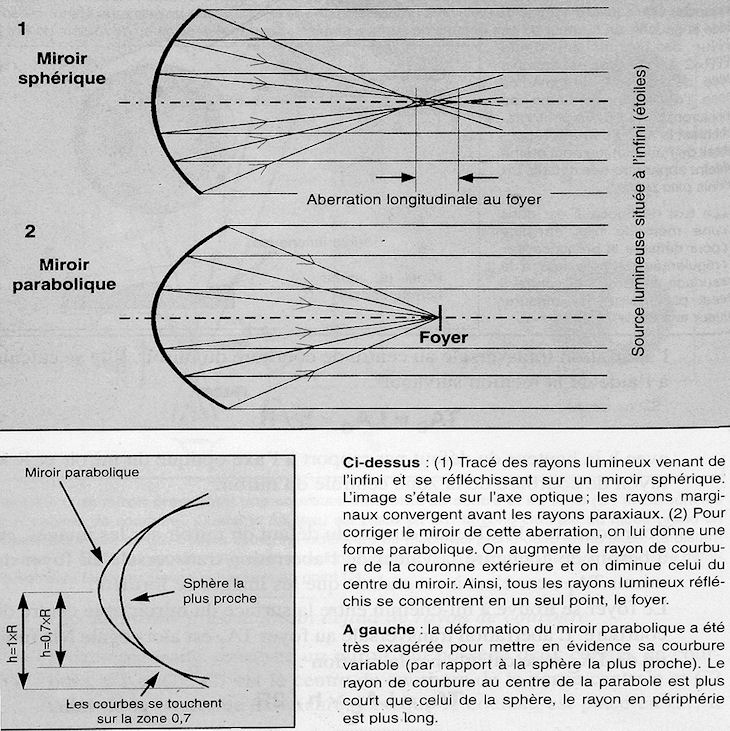
Nous avons donc un miroir sphérique capable de donner à son centre de courbure une image nette d'un objet placé également à ce centre de courbure. Mais en astronomie les objets sont à une distance infiniment grande. Les rayons lumineux qui en proviennent sont parallèles. Ceux qui tombent sur la périphérie du miroir se concentrent en un point plus proche du miroir que ceux qui tombent près de son centre. C'est l'aberration de sphéricité. Les photos et leurs commentaires montrent très bien le phénomène.

On voit qu'il faut donc évaser la sphère à son pourtour et la creuser en son centre. Rassurez- vous, il est question ici de micron ou de fraction de micron. Mais justement quelle tolérance peut-on admettre ? Longtemps on a cru qu'il suffisait d'améliorer la qualité des optiques en astronomie ou en microscopie pour atteindre des grossissements plus élevés. Il a fallu comprendre la nature ondulatoire de la lumière et les phénomènes de diffraction pour se rendre compte qu'il y a une limite théorique infranchissable.

Sans entrer dans un développement rébarbatif, il faut savoir que cette limite dépend uniquement du rapport entre la longueur focale d'un objectif et son diamètre. Ainsi des rayons lumineux strictement parallèles ne peuvent pas être concentrés mieux que dans une tache, appelée tache de diffraction, dont le rayon est donné par la formule r = 1,22 x L x F/D dans laquelle r est le rayon de la tache de diffraction, L est la longueur d'onde de la lumière soit 0,56 micron pour la lumière correspondant à la plus grande sensibilité de l'œil humain, F la longueur focale de l'objectif et D son diamètre.

Pour notre miroir au rapport F/D = 8, cela conduit à une tache de diffraction d'un rayon de 5,5 microns. Ce miroir sera donc parfait si tous les rayons qu'il reçoit sont concentrés dans une tache de 5,5 microns de rayon. Il est impossible de faire mieux. On voit pourquoi un miroir de 150 mm de diamètre ouvert à 8 est facile à faire mais qu'un miroir de 300 mm, que pour des raisons d'encombrement, on est conduit à ouvrir à 4 est beaucoup plus difficile à tailler car donnant une tache de diffraction de seulement 2,7 microns de rayon. Imaginez quel défaut minime de la courbure du miroir suffit, à 1,20 m de distance, pour rejeter un rayon lumineux en dehors de cette tache de diffraction.

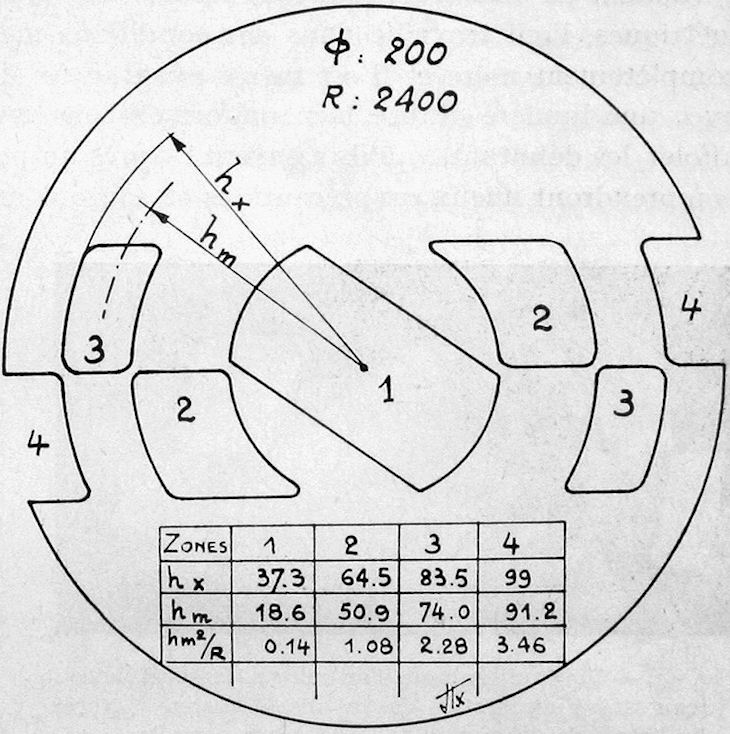
Le principe de la méthode de contrôle de la parabolisation d'un miroir, à partir de quelques zones judicieusement choisies, va donc être en ayant placé la fente lumineuse de l'appareil de Foucault au centre de courbure du miroir, de mesurer l'allongement de la distance au miroir, de l'image de cette fente. Il suffira de comparer cette distance à celle que l'on aura préalablement calculée pour une parabole exacte. La mesure en est facile car les centièmes de micron sur le verre donnent des mm sur le déplacement du couteau de l'appareil de Foucault. L'application de ce principe est facilitée par le fait que la méthode de taille des miroirs que nous avons décrite conduit à ce que des défauts éventuels résiduels soient forcément de révolution. Il est donc inutile de contrôler le miroir sur des zones entièrement circulaires, il suffit de le contrôler sur des petites fenêtres que l'on pratiquera dans un écran en carton léger placé devant le miroir.

Pratiquement la parabolisation en partant d'un miroir sphérique est obtenue par un travail comme lors du polissage mais avec des courses et des déports pouvant aller jusqu'à 4/5 du diamètre. Au bout d'une dizaine de minutes, on effectuera un premier contrôle. Le but de la manœuvre consiste à obtenir pour chaque zone testée un éclairage identique des deux fenêtres symétriques en jouant sur la position longitudinale du couteau et sur sa pénétration dans le faisceau lumineux. Il est évident que si le couteau pénètre trop au point d'occulter tout le faisceau, l'ensemble du miroir sera noir. À l'inverse si le couteau ne coupe pas du tout le faisceau, le miroir sera entièrement blanc. La position du couteau qui donne la même teinte pour deux fenêtres symétriques indique la valeur (hm²)/R de la zone concernée, à comparer à la valeur théorique calculée. Quand la parabolisation est bien amorcée, lavez le polissoir et le miroir sous un robinet. Laissez sécher puis continuez le travail avec de l'opaline à la place de l'oxyde de zirconium. L'opaline donnera un meilleur poli.

Le couteau est reculé successivement en partant de la zone centrale N°1 jusqu'à la zone externe N°6. Puis on dépasse un peu la zone N°6 pour refaire une autre série de mesures en revenant vers la zone N°1. Une bonne expérience dans cette pratique permet une concordance entre les deux séries de mesures à deux centièmes de mm près pour les zones 4, 5, 6 et trois à cinq centièmes près pour les zones 2 et 3. Pour la zone 1 la divergence peut atteindre plusieurs dixièmes de mm. Cela provient du fait que la mesure est moins sensible plus on s'approche du centre. Cela n'a pas de conséquence car justement la tolérance est d'autant plus grande que l'on s'approche du centre au point qu'elle peut atteindre plusieurs mm sur la zone 1. La tolérance acceptable pour chaque zone est donnée par la formule : T = ± (r x 2R)/hm dans laquelle r est le rayon de la tache de diffraction, R le rayon de courbure du miroir et hm est le rayon moyen de la zone concernée mesurée sur l'écran (c'est le hm ayant servi lors de la fabrication de l'écran).

Si toutes les mesures sont comprises dans cette tolérance (en ayant fait des mesures honnêtes sans tricher ou mieux en les faisant faire par un tiers impartial et expérimenté), le miroir est terminé. Dites-vous que le mieux est l'ennemi du bien et vouloir aller plus loin aboutit 9 fois sur 10 à une catastrophe et conduit à de longues et nombreuses retouches ne faisant qu'empirer le mal.

À noter que tel quel votre miroir donne d'excellentes images pour la lune et les étoiles brillantes. Vous pouvez faire tous les tests possibles sur une étoile brillante. Cependant il ne donnera sa pleine mesure sur le ciel profond que lorsqu'il aura été aluminé sous vide par une maison spécialisée dans cette entreprise. Il ne reste plus qu'à construire la partie mécanique, les informaticiens diraient le hard. Voilà encore de longues heures d'occupation.

Je me suis attaché à essayer de faire toucher du doigt le pourquoi plutôt que le comment faire qui n'aurait été que la recopie d'excellents ouvrages tels que :

• La construction du télescope d'amateur 2e édition de Jean Texereau (introuvable aujourd'hui)
• Réalisez votre télescope de Jean- Marc Lecleire
• Mon télescope et mon observatoire, pourquoi pas ? de Pierre Bourge et Jean Marc Becker.

J'espère que les auteurs me pardonneront d'avoir utilisé quelques images que ces livres contiennent, mais c'est pour la bonne cause.René Paris, promotion 50-53+R.